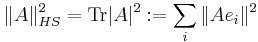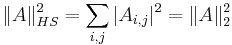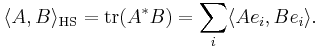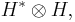Hilbert–Schmidt operator

In mathematics, a Hilbert–Schmidt operator, named for David Hilbert and Erhard Schmidt, is a bounded operator A on a Hilbert space H with finite Hilbert–Schmidt norm

$\|A\|^2_{HS}={\rm Tr} |A|^2:= \sum_{i} \|Ae_i\|^2$

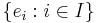where $\|\ \|$ is the norm of H and $\{e_i�: i\in I\}$ an orthonormal basis of H for an index set $I$ ^[1]^[2]. Note that the index set need not be countable. This definition is independent of the choice of the basis, and therefore

$\|A\|^2_{HS}=\sum_{i,j} |A_{i,j}|^2 = \|A\|^2_2$

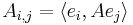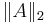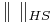for $A_{i,j}=\langle e_i, Ae_j \rangle$ and $\|A\|_2$ the Schatten norm of $A$ . In Euclidean space $\|\ \|_{HS}$ is also called Frobenius norm.

The product of two Hilbert–Schmidt operators has finite trace class norm; therefore, if A and B are two Hilbert–Schmidt operators, the Hilbert–Schmidt inner product can be defined as

$\langle A,B \rangle_\mathrm{HS} = \operatorname{tr} (A^*B) = \sum_{i} \langle Ae_i, Be_i \rangle.$

The Hilbert–Schmidt operators form a two-sided *-ideal in the Banach algebra of bounded operators on H. They also form a Hilbert space, which can be shown to be naturally isometrically isomorphic to the tensor product of Hilbert spaces

$H^* \otimes H, \,$

where H* is the dual space of H.

The Hilbert–Schmidt operators are closed in the norm topology if, and only if, H is finite dimensional.

An important class of examples is provided by Hilbert–Schmidt integral operators.

References

^ Moslehian, M.S.. "Hilbert–Schmidt Operator (From MathWorld)". http://mathworld.wolfram.com/Hilbert-SchmidtOperator.html.
^ Voitsekhovskii, M.I. (2001), "Hilbert–Schmidt operator", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=H/h047350